Demostración de Identidades Trigonométricas con ejemplos resueltos paso a paso

Demostración de Identidades Trigonométricas con ejemplos resueltos paso a paso.

¿Qué es una Identidad Trigonométrica?

Son igualdades que contienen razones trigonométricas y que son verdaderas para cualquier valor de los ángulos siempre y cuando están definidos.

¿Qué procedimiento se debe seguir para demostrar una Identidad Trigonométrica?

Para demostrar que una igualdad es una identidad se sigue el siguiente procedimiento:

Cuando las razones trigonométricas del ángulo doble o del ángulo mitad se recomienda llevarlas todas ellas al ángulo normal por medio de las fórmulas respectivas.

Cuando las razones trigonométricas son de sumas o diferencia de ángulos se sustituye por sus fórmulas respectivas.

Si después de hacer las transformaciones indicadas anteriormente no aparecen ninguna simplificación es ventajoso cambiar las razones trigonométricas a seno o a coseno.

**

**

Métodos específicos para la demostración de Identidades Trigonométricas

Primer método: Este método consiste en efectuar operaciones en un solo miembro de la igualdad, haciendo las transformaciones correspondientes hasta llegar al valor del otro.

Segundo método: este método consiste en efectuar operaciones en los dos miembros de la igualdad, pero en forma independiente, hasta que los dos miembros sean iguales.

Cuando se sigue este método es necesario hacer las operaciones en cada miembro y no efectuar transformaciones como se hacen en las ecuaciones, es decir, no pueden pasarse términos de un miembro a otro, no pueden quitarse denominadores simultáneamente a los dos miembros de la igualdad, o, en otras palabras, no se puede actuar como si fuera una igualdad. pues lo que hay que demostrar es que lo es.

Identidades fundamentales y pitagóricas que se utilizan para la demostración de identidades trigonométricas

Tambien les dejaremos una tabla resumen de otras identidades

Al final del post les dejaré un link para que descargue estas tablas en formato pdf.

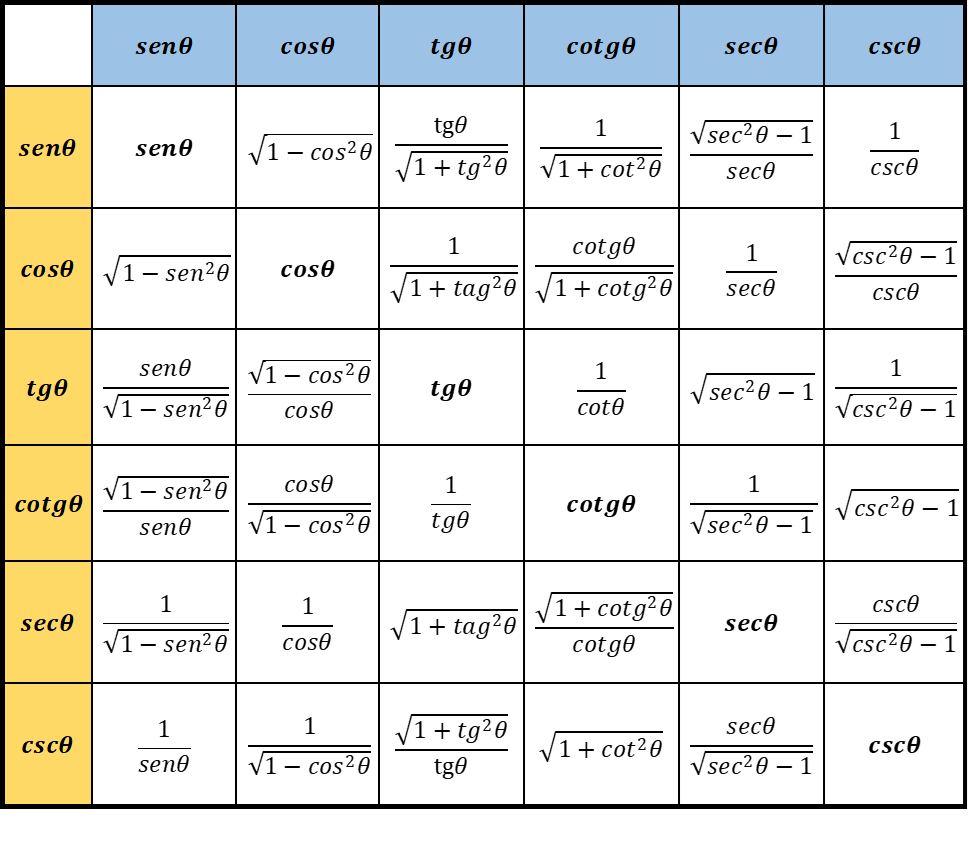
10 Recomendaciones prácticas para la demostración de identidades trigonométricas

✅Se deben aprender todas las identidades trigonométricas. Si no es el caso, deben tenerlas anotadas en una ficha o cualquier otro medio. Hay un link para descargarlas en formato pdf.

✅Se debe visualizar ambos lados de la igualdad y se debe empezar por la por la parte más compleja.

✅Siempre es recomendable pasar todas las razones trigonométricas en función de senos y cosenos. Es una práctica que se usa frecuentemente.

✅Se debe recordar siempre que solo se hacen simplificaciones, operaciones y transformaciones solo en un miembro de la igualdad. No se puede proceder como en las ecuaciones.

✅Frecuentemente se deben hacer sumas yrestas de fracciones heterogéneas, por lo que hay que estar familiarizado con estos procedimientos.

✅Hay que recordar el tema de productosnotables y factorización en todos sus casos.

✅Recordar casos de potenciación y simplificación de fracciones.

✅Siempre es recomendable pasar todas las razones trigonométricas en función de senos y cosenos. Es una práctica que se usa frecuentemente.

✅Muy importante: Se debe recordar siempre que solo se hacen simplificaciones, operaciones y transformaciones solo en un miembro de la igualdad. No se puede proceder como en las ecuaciones.

✅Recordar casos de potenciación y simplificación de fracciones.

36 Ejemplos resueltos paso a paso de la demostración de Identidades Trigonométricas

Ejemplo 1

Ejemplo 2

**

**

Ejemplo 3

Ejemplo 4

Ejemplo 5

Ejemplo 6

Ejemplo 7

**

**

Ejemplo 8

Ejemplo 9

Ejemplo 10

Ejemplo 11

Ejemplo 12

Ejemplo 13

**

**

Ejemplo 14

Ejemplo 15

Ejemplo 16

Ejemplo 17

**

**

Ejemplo 18

Ejemplo 19

Ejemplo 20

Ejemplo 21

Ejemplo 22

Ejemplo 23

**

**

Ejemplo 24

Ejemplo 25

Ejemplo 26

Ejemplo 27

Ejemplo 28

Ejemplo 29

Ejemplo 30

**

**

Ejemplo 31

Ejemplo 32

Ejemplo 33

Ejemplo 34

Ejemplo 35

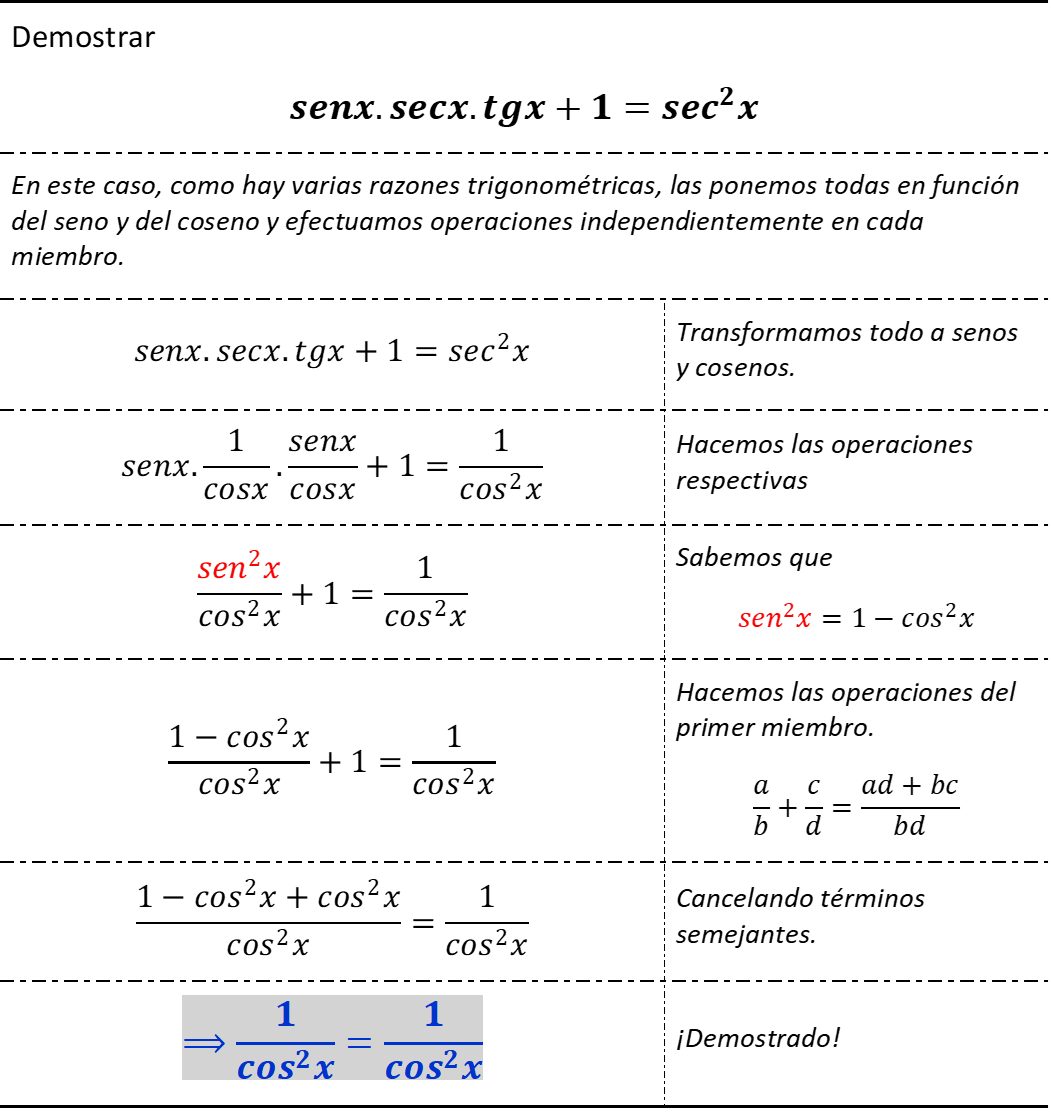
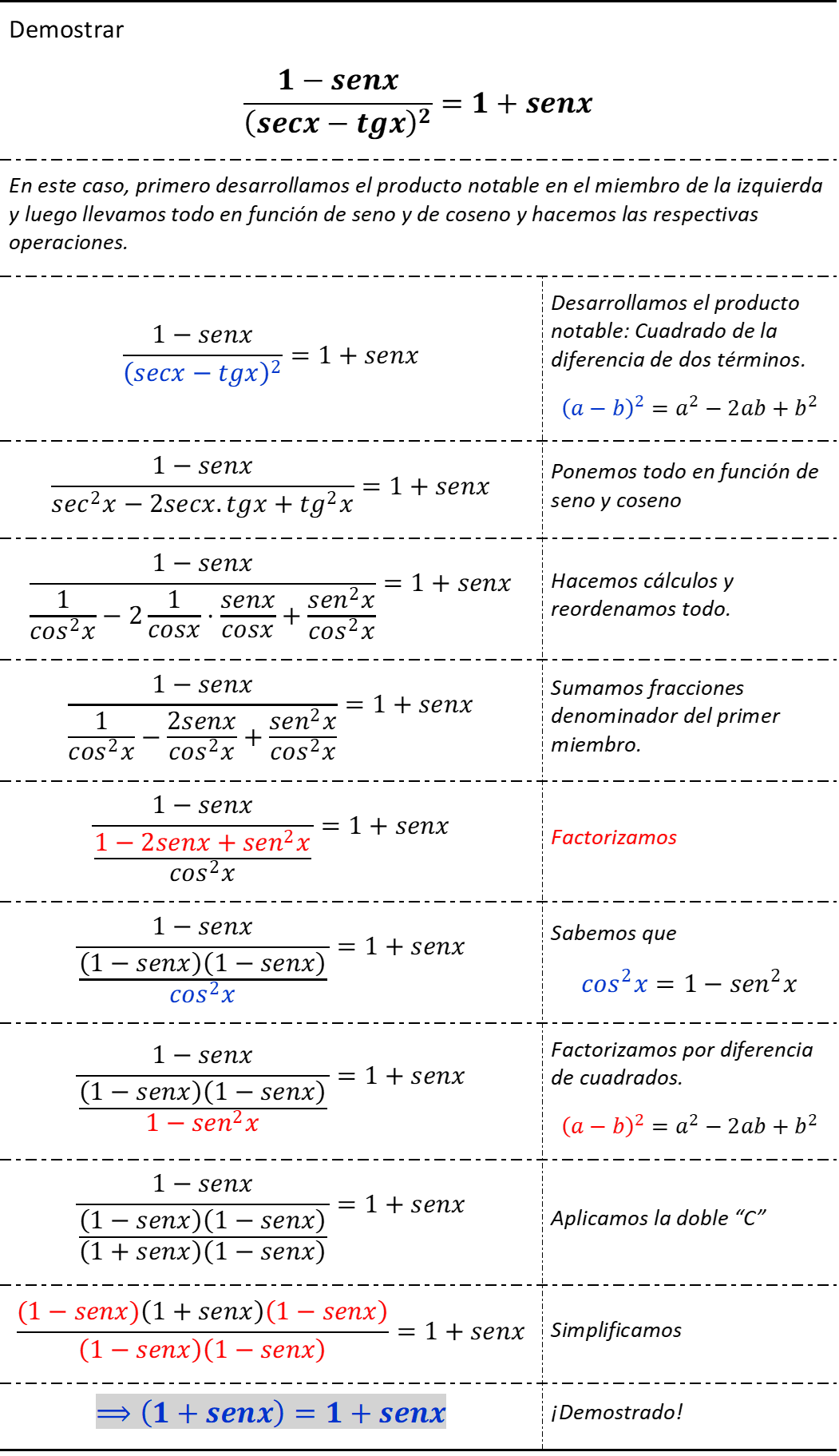
Ejemplo 36

Descargas:

IDENTIDADES TRIGONOMÉTRICAS PITAGORICAS, RECÍPROCAS Y ENTRE FUNCIONES. En formato pdf. Haga click aquí 

RESUMEN DE IDENTIDADES TRIGONOMÉTRICAS COMPLEMENTARIAS. En formato pdf. haga click aquí

SIGNOS DE LAS RAZONES TRIGONOMÉTRICAS. ÁNGULOS COMPLEMENTARIOS Y SUPLEMENTARIOS. En formato pdf. Haga click aquí.

RAZONES TRIGONOMÉTRICAS DE ÁNGULO DOBLE, ÁNGULO TRIPLE, SUMA Y RESTA DE DOS ÁNGULOS. En formato pdf. haga click aquí.

Dios les bendiga grandemente.