Sistema de ecuaciones lineales
¿Qué es una ecuación lineal?
Podemos definir una ecuación lineal con una incógnita a aquella en que la incógnita está elevada al exponente uno.
Ejemplo: 2x+1 = 7.
¿En qué consiste resolver una ecuación lineal?
Resolver una ecuación lineal con una incógnita es encontrar el único valor de la incógnita que transforma la ecuación en una identidad.
Ecuación lineal con dos incógnitas
Una ecuación lineal con dos incógnitas es aquella en que las incógnitas están elevadas a uno; ejemplo: 3x+2y = 8
Resolver una ecuación lineal con dos incógnitas es encontrar un PAR de números. de los infinitos que pueden formarse, que sustituidos en la ecuación la transforman en una identidad.
Para resolver una ecuación lineal con dos incógnitas es necesario dar valores arbitrarios a una de las incógnitas, que llamamos variable independiente (generalmente la x), que sustituido en la ecuación la transforma en una ecuación con una incógnita; por ejemplo:
**
**
Ecuaciones equivalentes:
Dos o más ecuaciones son equivalentes cuando tienen las mismas soluciones. Cuando una ecuación la transformamos en otra, bien por quitar denominadores, o por agrupar términos semejantes, o por despejar una de las incógnitas, cada una de las ecuaciones que obtenemos es equivalente a la dada.
El objeto de obtener ecuaciones equivalentes es hacer que una ecuación dada se escriba en forma más sencilla.
¿Qué es un sistema de ecuaciones?
Un sistema de ecuaciones es el conjunto formado por varias ecuaciones, cuyo objeto es hallar las soluciones que son comunes a todas ellas.
Para anotar que varias ecuaciones forman un sistema se las escribe a todas ellas después de una llave.
¿A qué llamamos solución de un sistema de ecuaciones?
Decimos que la Solución de un sistema es el valor de las incógnitas que satisfacen simultáneamente a todas las ecuaciones que forman el sistema.
Resolver un sistema es el proceso que se emplea para hallar la solución del mismo.
Respecto a la solución del sistema hay varios casos.
✅El sistema es COMPATIBLE cuando entre todas las soluciones de cada ecuación hay una o varias soluciones comunes.
✅Cuando el sistema solamente tiene una solución común a todas ellas, decimos que el sistema es COMPATIBLE DETERMINADO.
✅Cuando el sistema tiene infinitas soluciones comunes a todas ellas decimos que es COMPATIBLE INDETERMINADO.
✅El sistema es INCOMPATIBLE cuando entre todas las soluciones de cada una de las ecuaciones que forman el sistema no hay solución común.
Métodos de Resolución de sistemas de dos ecuaciones con dos incógnitas
1.- Método de Reducción
¿En que consiste el método de reducción?
Este método consiste en hacer las transformaciones necesarias para que el sistema formado por dos ecuaciones con dos incógnitas se transforme en una ecuación con una incógnita, para lo cual nos apoyamos en las siguientes propiedades:
👉Si a una ecuación la multiplicamos o dividimos por un número resulta una ecuación equivalente, es decir, que tiene las mismas soluciones.
👉Si sumamos miembro a miembro dos ecuaciones resulta otra ecuación equivalente a estas dos.
Forma de resolver un sistema por el método de reducción
✅Elegimos la incógnita que vamos a eliminar y multiplicamos o dividimos la o las ecuaciones por las cantidades que sean necesarias para que los coeficientes sean iguales pero de signo contrario.
✅Sumamos miembro a miembro las dos ecuaciones para que la incógnita se anule.
✅Resolvemos la ecuación resultante.
✅Calculamos el valor de la otra incógnita.
Ejercicios resueltos paso a paso de sistemas de ecuaciones por el MÉTODO DE REDUCCIÓN
EJEMPLO 1
La solución gráfica del sistema de ecuaciones queda representado de la siguiente manera:
**
**
EJEMPLO 2
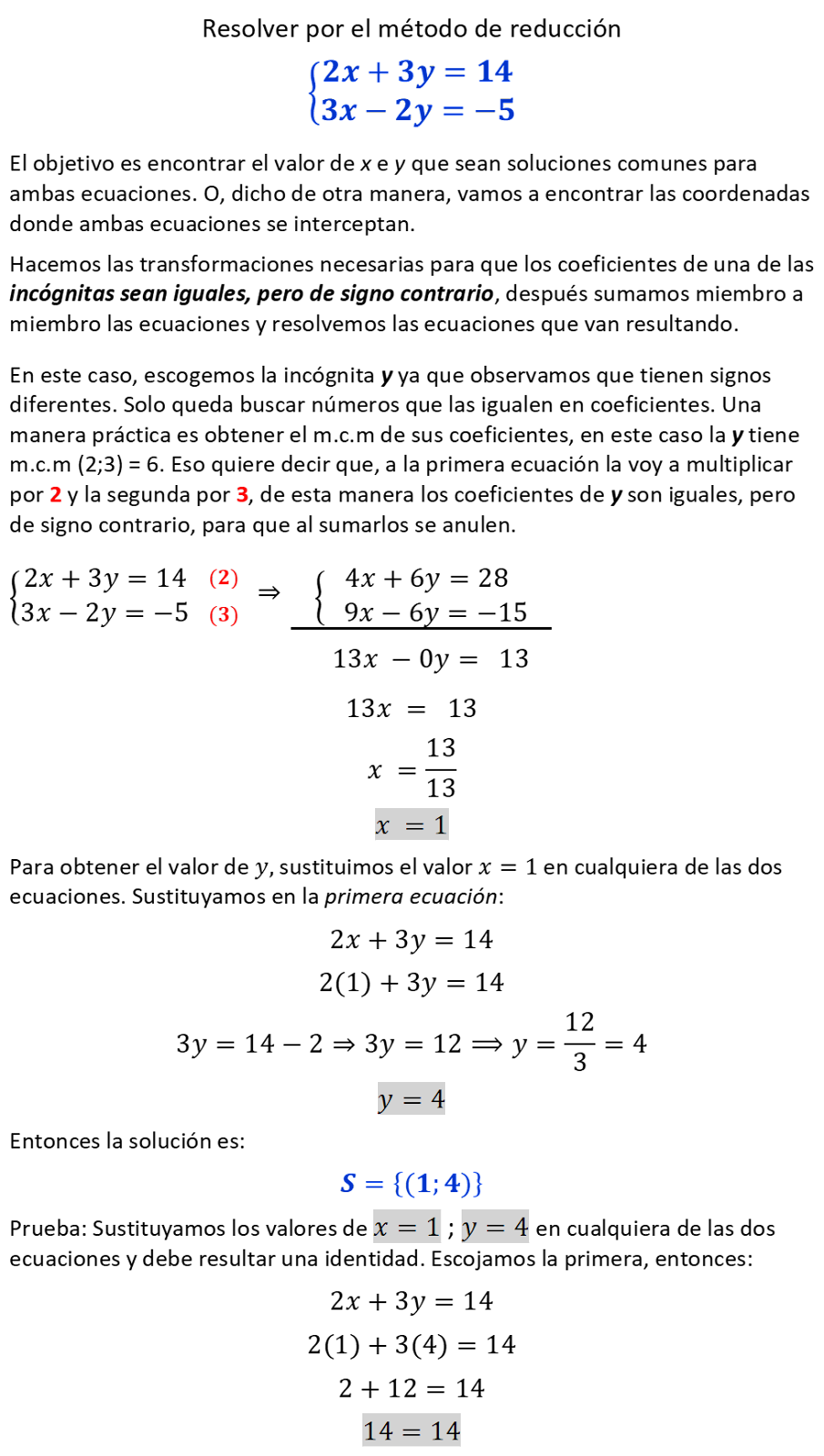
La solución gráfica del sistema de ecuaciones queda representado de la siguiente manera:
EJEMPLO 3
EJEMPLO 4
La solución gráfica del sistema de ecuaciones queda representado de la siguiente manera:
**
**
EJEMPLO 5
La solución gráfica del sistema de ecuaciones queda representado de la siguiente manera:
**
**
2.- Método de Sustitución
¿En que consiste el método de sustitución?
Consiste en despejar una de las incógnitas y su valor se sustituye en la otra ecuación, con lo cual llegamos a una ecuación con una incógnita.Este método es muy laborioso, pero en determinados casos es muy práctico.
Ejercicios resueltos paso a paso de sistemas de ecuaciones por el MÉTODO DE SUSTITUCIÓN
EJEMPLO 6
La representación gráfica del sistema de ecuaciones
EJEMPLO 7
EJEMPLO 8
**
**
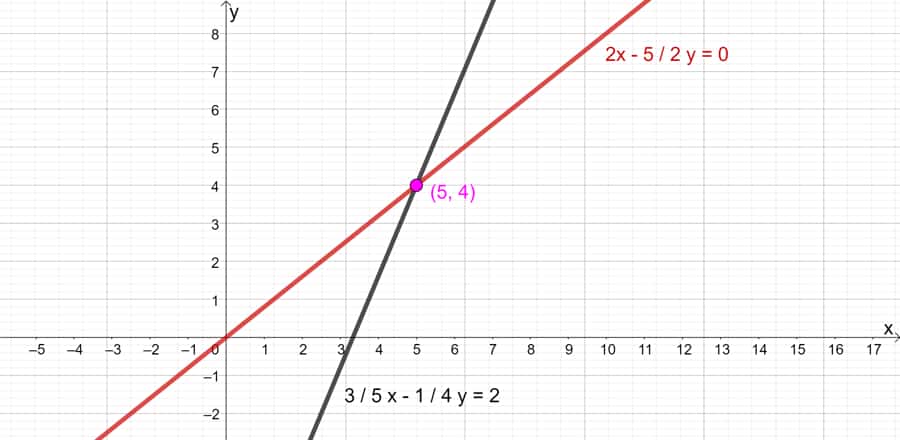
EJEMPLO 9
La representación gráfica del sistema de ecuaciones
La representación gráfica del sistema de ecuaciones
EJEMPLO 11
La representación gráfica del sistema de ecuaciones
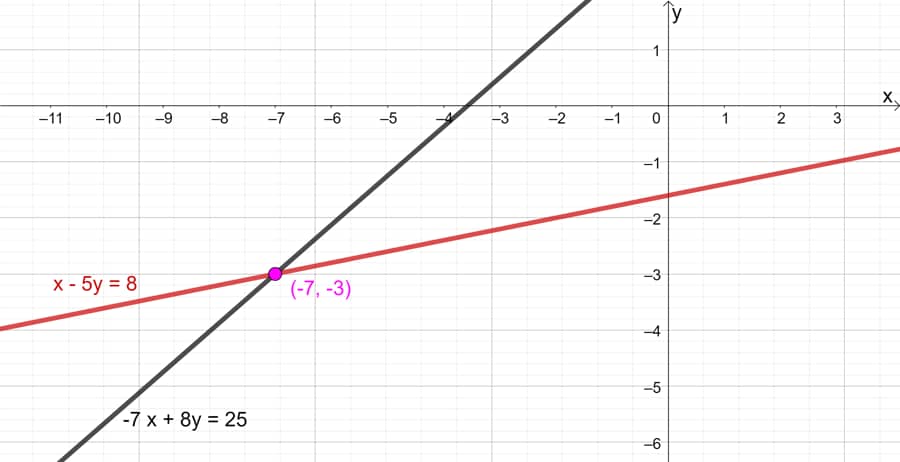
EJEMPLO 12
La representación gráfica del sistema de ecuaciones
**
**
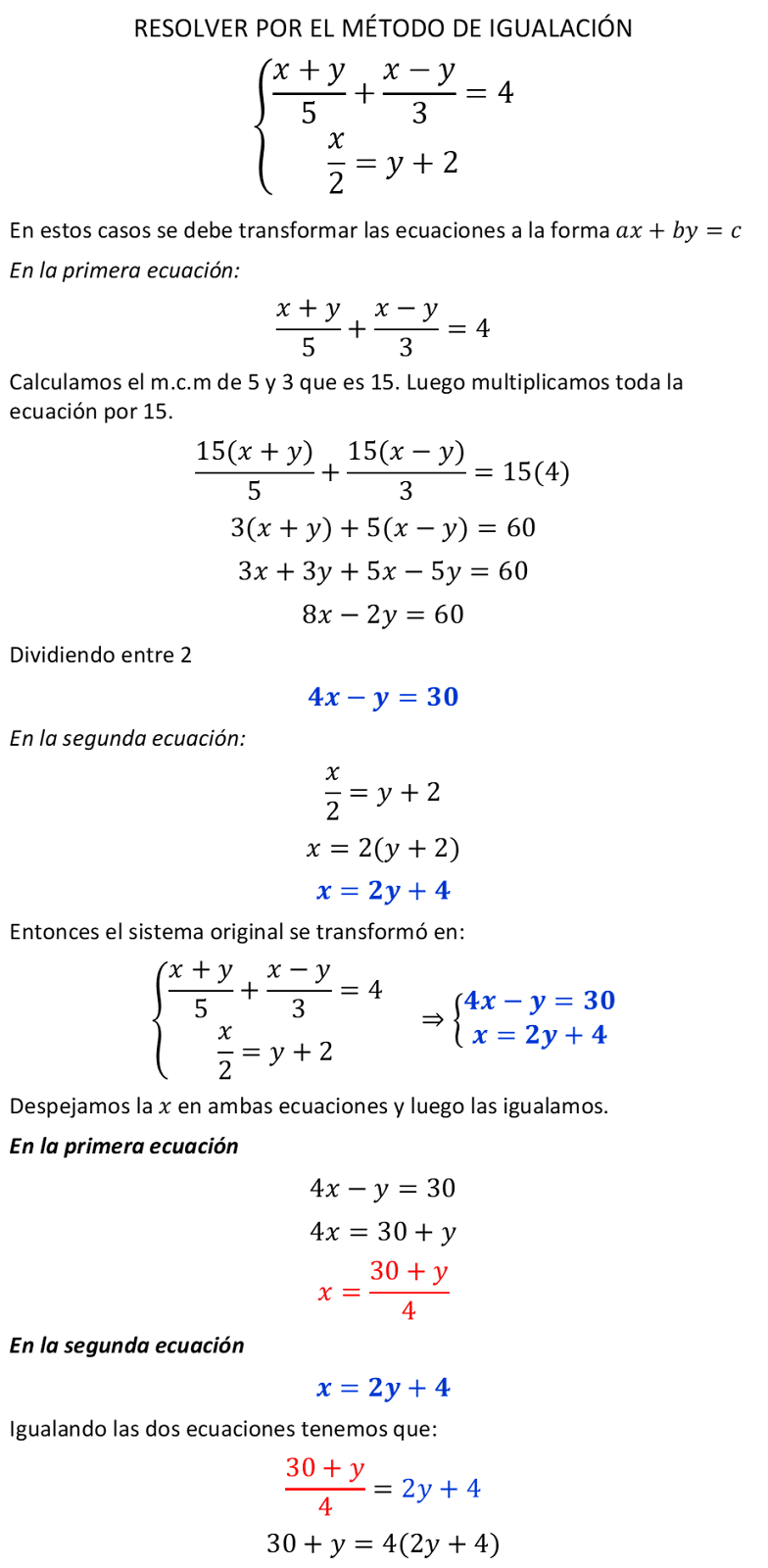
3.- Método de Igualación
Ejercicios resueltos paso a paso de sistemas de ecuaciones por el MÉTODO DE IGUALACIÓN
EJEMPLO 13
La representación gráfica del sistema de ecuaciones
EJEMPLO 14
**
**
EJEMPLO 15
La representación gráfica del sistema de ecuaciones
Si te ha sido de utilidad este post le agradecería que lo compartas en tus redes sociales y así me estaría ayudando para crear nuevos contenidos. Saludos.
No hay comentarios:
Publicar un comentario
Escriba su comentario de tal manera que éste sea suficientemente claro. No utilice argumentos que incluyan ataques personales o comentarios relacionados con otra persona. Los comentarios contribuyen a una discusión justa. Trate a los otros usuarios de la misma manera que quisiera que lo trataran a usted. Los comentarios se referirán a la entrada del blog correspondiente o a comentarios previos. No se aceptarán comentarios difamatorios, racistas, ofensivos, inadecuados, desproporcionadamente largos y temáticamente irrelevantes, así como comentarios destinados principalmente a la transmisión de propaganda, publicidad o a la divulgación de ideologías.
El Administrador del Blog.
.